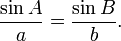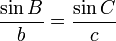love_matematicku

Kamis, 26 Februari 2009

Fungsi eksponensial adalah salah satu fungsi yang paling penting dalam matematika. Biasanya, fungsi ini ditulis dengan notasi exp(x) atau e^x, dimana e adalah basis logaritma natural yang kira-kira sama dengan 2.71828183.

Fungsi eksponensial (merah) terlihat hampir mendatar horizontal (naik secara sangat perlahan) untuk nilai x yang negatif, dan naik secara cepat untuk nilai x yang positif.

Sebagai fungsi variabel bilangan real x, grafik e^x selalu positif (berada diatas sumbu x) dan nilainya bertambah (dilihat dari kiri ke kanan). Grafiknya tidak menyentuh sumbu x, namun mendekati sumbu tersebut secara asimptotik. Invers dari fungsi ini, logaritma natural, atau ln(x), didefinisikan untuk nilai x yang positif.

Secara umum, variabel x dapat berupa bilangan real atau bilangan kompleks, ataupun objek matematik

Sifat-sifat

Dengan menggunakan logaritma natural, fungsi eksponensial yang lebih generik dapat didefinisikan. Fungsi

$\!\, a^x=e^{x \ln a}$

yang terdefinisikan untuk a > 0, dan semua bilangan real x, disebut juga fungsi eksponensial dengan basis a.

Perlu diperhatikan bahwa persamaan tersebut berlaku pula untuk a = e, karena

$\!\, e^{x \ln e}=e^{x \cdot 1}=e^x.$

Fungsi eksponensial dapat "menterjemahkan" antara dua macam operasi, penjumlahan dan pengkalian. Ini dapat dilihat dari rumus-rumus eksponen sebagai berikut:

$\!\, a^0 = 1$

$\!\, a^1 = a$

$\!\, a^{x + y} = a^x a^y$

$\!\, a^{x y} = \left( a^x \right)^y$

$\!\, {1 \over a^x} = \left({1 \over a}\right)^x = a^{-x}$

$\!\, a^x b^x = (a b)^x$

Rumus-rumus diatas berlaku untuk semua bilangan real positif a dan b dan semua bilangan real x dan y. Ekspresi yang mengandung pecahan dan pengakaran pada umumnya dapat disederhanakan dengan menggunakan notasi eksponensial, karena:

${1 \over a} = a^{-1}$

dan, untuk semua a > 0, bilangan real b, dan bilangan bulat n > 1:

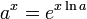
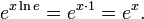
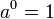
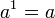
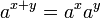
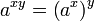
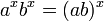
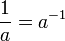
$\sqrt[n]{a^b} = \left(\sqrt[n]{a}\right)^b = a^{b/n}$

eksponensial

Jumat, 20 Februari 2009

hii gilani

Terang bersinar kulit putihmu
Hitam dan panjang urai rambutmu
Harum semerbak wangi parfummu
...
Hii... takuuutt...
Hantuuuuuu.......

wanita idaman

Laksana rembulan...
Menyinari insan bumi.

Jika ia memandang...
Dunia seakan tergetar karena ketulusannya
Jika ia berkata...
Dunia seakan terlena karena kelembutannya.
Jika ia tersenyum...
Duniapun ikut tersenyum karena keikhlasannya.

Laksana pelita...
Tubuh terbakar demi sebuah pengorbanan.
Menjadi penuntun di tengah gemerlapnya dunia.

Laksana sahabiyah...
Langkah kakinya bagai langkah Fatimah.
Hidupnya penuh ketenangan jiwa.
Karena hatinya selalu berdzikir.

Dialah wanita sholehah..
Yang senantiasa menjadi penentu.
Akan sebuah perubahan dunia.

Tangen (bahasa Belanda: tangens; lambang tg, tan) dalam matematika adalah perbandingan sisi segitiga yang ada di depan sudut dengan sisi segitiga yang terletak di sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga di kanan; berdasarkan definisi tangen di atas maka nilai tangen adalah

$\tan A = {\mbox{a} \over \mbox{b}} \qquad \tan B = {\mbox{b} \over \mbox{a}}$

Nilai tangen positif di kuadran I dan III dan negatif di kuadran II dan IV.

Hubungan Nilai Tangen dengan Nilai Sinus dan Cosinus

$\tan A = \frac{Sin A}{Cos A}\,$

Nilai Tangen Sudut Istimewa

$\tan 0^o = 0\,$

$\tan 15^o = 2 - \sqrt {3},$

$\tan 30^o = \frac{\sqrt {3}}{3}\,$

$\tan 37^o = \frac{3}{4}\,$

$\tan 45^o = 1\,$

$\tan 53^o = \frac{4}{3}\,$

$\tan 60^o = \sqrt{3}\,$

$\tan 75^o = 2 + \sqrt {3},$

$\tan 90^o = \infty\,$

Kosekan

Kosekan (disimbolkan dengan cosec atau csc) dalam matematika adalah perbandingan sisi miring segitiga dengan sisi yang terletak di depan sudut (dengan catatan bahwa segitiga itu adalah segitiga siku-siku atau salah satu sudut segitiga itu 90^o). Perhatikan segitiga di kanan; berdasarkan definisi kosekan di atas maka nilai kosekan adalah

$\csc A = {\mbox{c} \over \mbox{a}} \qquad \csc B = {\mbox{c} \over \mbox{b}}$

Hubungan kosekan dengan sinus:

$\csc A = \frac{1}{\sin A}\,$

Tabel Kosekan

Sudut	Nilai Kosekan
0°	~
30°	2
45°	1,4143
60	0,94287
90°	1

hukum sinus

Dalam trigonometri, hukum sinus ialah pernyataan tentang segitiga yang berubah-ubah di udara. Jika sisi segitiga ialah (kasus sederhana) a, b dan c dan sudut yang berhadapan bersisi (huruf besar) A, B and C, hukum sinus menyatakan

${\sin A \over a}={\sin B \over b}={\sin C \over c}.\,$

Rumus ini berguna menghitung sisi yang tersisa dari segitiga jika 2 sudut dan 1 sisinya diketahui, masalah umum dalam teknik triangulasi. Dapat juga digunakan saat 2 sisi dan 1 dari sudut yang tak dilampirkan diketahui; dalam kasus ini, rumus ini dapat memberikan 2 nilai penting untuk sudut yang dilampirkan. Saat ini terjadi, sering hanya 1 hasil akan menyebabkan seluruh sudut kurang daripada 180°; dalam kasus lain, ada 2 penyelesaian valid pada segitiga.

Timbal balik bilangan yang yang digambarkan dengan hukum sinus (yakni a/sin(A)) sama dengan diameter d . Kemudian hukum ini dapat dituliskan

${a \over \sin A }={b \over \sin B }={c \over \sin C } = d.$

Dapat ditunjukkan bahwa:

$d = \frac{abc} {2\sqrt{s(s-a)(s-b)(s-c)}} = \frac {2abc} {\sqrt{(a^2+b^2+c^2)^2+2(a^4+b^4+c^4) }}$

di mana

s merupakan semi-perimeter

$s = \frac{(a+b+c)} {2}$

Turunan

Buatlah segitiga dengan sisi a, b, dan c, dan sudut yang berlawanan A, B, dan C. Buatlah garis dari sudut C pada sisi lawannya c yang menonjol sekali dalam 2 segitiga siku-siku, dan sebut panjang garis ini h.

Dapat diamati bahwa: